정보처리기사 제1과목 데이터베이스 – 제2장 자료구조의 기본 2부
요약 정리
Ⅲ. 정렬, 탐색기법
1. 정렬(Sort)
가. 정렬(Sort)의 정의
각 레코드의 특정한 부분을 키로 정하고, 키의 값에 따라 오름차순이나 내림차순으로 파일의 레코드를 재배열하는 작업을 말한다.
나. 정렬(Sort) 장소에 따른 분류
일반적으로 정렬(Sort)은 주기억장치 내에서 수행되는 내부 정렬(Internal Sort) 방식과 내부 정렬(Internal Sort)의 결과를 보조기억장치에 넣은 후, 여러 개의 부분 파일을 합병해서 처리하는 외부 정렬(External Sort)이 있다.
① 내부 정렬(Internal Sort)
– 내부 정렬(Internal Sort)의 개념
정렬하고자 하는 자료를 주기억장치에 가져다 놓고 고속으로 정렬하는 방식으로 자료의 양이 적을 때 사용한다
– 내부 정렬(Internal Sort)의 종류
- 삽입 정렬(Insertion Sort): 대상 자료가 일부 정렬되어 있을 때 유리한 정렬 방식으로 선택된 키 값을 앞쪽 자료들의 키 값과 비교하여 자신의 위치를 찾아 삽입하여 정렬시키는 방식. 연산 시간 O(n2).
삽입 정렬(Insertion Sort) 알고리즘
#include
int insertion_sort(int *ay, int length) { int i, j, pos, temp; /** 배열의 길이 많큼 아래로 이동 */ for (i = 0; i < length; i++) { temp = ay[i]; // 키 값을 temp에 할당 pos = i – 1; // 이전 값 /** 배열의 크기를 넘지 않고, 이전 값이 키 값 보다 클 경우 */ while (pos >= 0 && ay[pos] > temp) { ay[pos+1] = ay[pos]; // 이전 값을 다음 값에 할당 pos–; } ay[pos+1] = temp; // 키 값을 다음 값에 할당 /** 출력 */ for (j = 0; j < i + 1; j++) { printf("%d ", ay[j]); printf("\n"); } } void main(void) { int ay[] = {77, 33, 44, 11, 88, 22, 66, 55}; int lenth; length = sizeof(ay)/2; insertion_sort(ay, length); } Result
초 기 값: 77 33 44 11 88 22 66 55 i=0 일때: 77 i=1 일때: 33 77 i=2 일때: 33 44 77 i=3 일때: 11 33 44 77 i=4 일때: 11 33 44 77 88 i=5 일때: 11 22 33 44 77 88 i=6 일때: 11 22 33 44 66 77 88 i=7 일때: 11 22 33 44 55 66 77 88
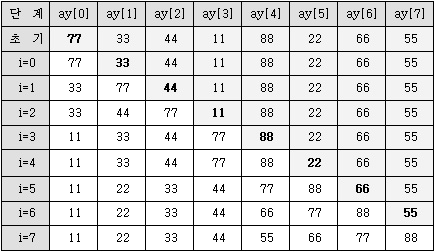
삽입 정렬(Insertion Sort) 수행 과정
i=0일 때 키 값인 77이 이전 값보다 크기 때문에 교환은 발생하지 않는다. i=1일 때 키 값인 33과 이전 값인 77과 비교 후 교환 발생. i=2일 때 키 값인 44와 이전 값인 77과 비교 후 교환 발생. i=3일 때 키 값인 11과 이전 값인 77과 비교 후 교환 발생. 키 값인 11과 이전 값인 44와 비교 후 교환 발생. 키 값인 11과 이전 값인 33과 비교 후 교환 발생. 이후 동일. - 버블 정렬(Bubble Sort): 인접한 두 키를 비교하면서 교환하여 정렬하되, 단계별로 수행하면서 각 단계 수행 중 교환이 일어나지 않으면 정렬이 완료된 것으로 더 이상의 단계를 수행하지 않고 종료시켜 정렬을 완료시키는 방식. 리스트 중에서 가장 가벼운(작은) 항목이 물속의 거품(bubble)처럼 가장 위로 상승하고, 그 다음 가벼운 것이 다음 자리로 상승하여 가장 무거운 것이 끝자리로 오기 때문에 이 이름이 붙었다. 연산 시간 O(n2).
버블 정렬(Bubble Sort) 알고리즘
#include
#define TRUE (1==1) #define FALSE (!TRUE) /** 교환 함수 */ void interchange(int &a, int &b) { int temp = a; a = b; b = temp; } void bubble_sort(int *ay, int length) { int j; int flag; do { flag = FALSE; /** 키 값을 다음 값과 비교하여 다음 값 보다 크다면 교환 */ for (j = 0; j < length - 1; j++) { /** 키 값이 다음 값 보다 클 경우 */ if (ay[j] > ay[j+1]) { interchange(ay[j], ay[j+1]); // 교환 함수 호출 flag = TRUE; } } /** 출력 */ for (j = 0; j < length; j++) printf("%d", ay[j]); printf("\n"); } while(flag); } void main() { int ay[] = {25, 52, 48, 37, 17, 92, 86, 33}; int length; length = sizeof(ay) / 2; bubble_sort(ay, length); } Result
초기값: 25 52 48 37 17 92 86 33 1 단계: 25 48 37 17 52 86 33 92 2 단계: 25 37 17 48 52 33 86 92 3 단계: 25 17 37 48 33 52 86 92 4 단계: 25 17 37 48 33 52 86 92 5 단계: 17 25 37 33 48 52 86 92 6 단계: 17 25 33 37 48 52 86 92 7 단계: 17 25 33 37 48 52 86 92
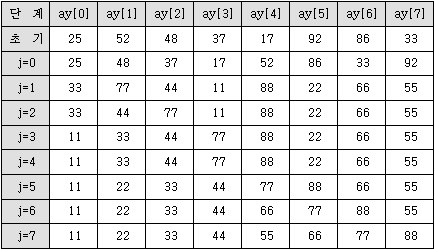
버블 정렬(Bubble Sort) 수행 과정 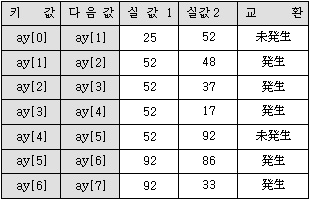
j=0일 때 수행 과정 j=0일 때 키 값인 25이 다음 값인 52 보다 작기 때문에 교환은 발생하지 않음. 키 값인 52와 다음 값인 48과 비교 후 교환 발생. 키 값인 52와 다음 값인 37과 비교 후 교환 발생. 키 값인 52와 다음 값인 17과 비교 후 교환 발생. 키 값인 52는 다음 값인 92 보다 작기 때문에 교환은 발생하지 않음. 키 값인 92와 다음 값인 86과 비교 후 교환 발생. 키 값인 92와 다음 값인 33과 비교 후 교환 발생. 이후 동일.
- 선택 정렬(Selection Sort): 전체 자료 중에서 최소값을 찾아, 처음 키 값부터 순차적으로 교환하여 정렬하는 방식. 삽입 정렬(Insertion Sort)이나 버블 정렬(Bubble Sort) 보다 이동 횟수가 준다는 것이 특징이다. 연산시간 O(n2).
선택 정렬(Selection Sort) 알고리즘
#include
/** 교환 함수 */ void interchange(int &a, int &b) { int temp = a; a = b; b = temp; } void selection_sort(int *ay, int length) { int i, j, min_index; for (i = 0; i < length-1; i++) { min_index = i; /** 우측으로 이동하며 키 값과 비교 값을 비교하여 최소 값을 구함 */ for (j = i+1; j < length; j++) { /** 키 값이 비교 값 보다 클 경우 */ if (ay[j] < ay[min_index]) { min_index = j; // 키 값을 비교 값에 할당 } } /** 배열의 위치와 현재의 최소 값의 위치가 같지 않을 경우 */ if (i != min_index) { interchange(ay[i], ay[min_index]); // 교환 함수 호출 } /** 출력 */ for (j = 0; j < length; j++) printf("%d", ay[j]); printf("\n"); } } void main() { int ay[] = {77, 33, 44, 11, 88, 22, 66, 55}; int length; length = sizeof(ay) / 2; selection_sort(ay, length); } Result
최 초 값: 77 33 44 11 88 22 66 55 i=0 일때: 11 33 44 77 88 22 66 55 i=1 일때: 11 22 44 77 88 33 66 55 i=2 일때: 11 22 33 77 88 44 66 55 i=3 일때: 11 22 33 44 88 77 66 55 i=4 일때: 11 22 33 44 55 77 66 88 i=5 일때: 11 22 33 44 55 66 77 88
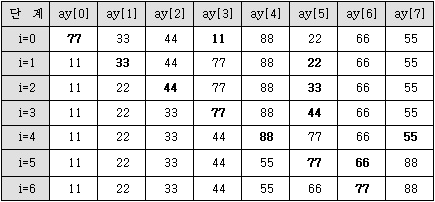
선택 정렬(Selection Sort) 수행 과정
i=0일 때 최소값인 11을 찾아 처음 키 값인 77과 비교 후 교환. i=1일 때 최소값인 22를 찾아 순차적으로 33과 비교 후 교환. i=2일 때 최소값인 33을 찾아 순차적으로 44와 비교 후 교환한다. 이후 동일. - 쉘 정렬(Shell Sort): 쉘 정렬(Shell Sort)은 삽입 정렬(Insertion Sort)의 확장된 개념으로 삽입 정렬에서는 데이터가 이미 정렬되어 있는 경우에는 비교하지 않으므로 정렬 간격을 축소시켜 가면서 데이터를 미리 듬성듬성 정렬하여 놓고 삽입 정렬하는 방식. 연산 시간 O(n5/3).
- 퀵 정렬(Quick Sort): 첫 번째 데이터를 중간 키 값으로 설정하고, 좌측에는 키 값보다 그 중간 값을 대상 자료 중 적당한 위치에 위치시켜 대상 자료를 부분적으로 나누어가면서 되 부름 방식으로 반복 분류시켜 정렬하는 방식. 퀵 정렬(Quick Sort)은 가장 빠른 정렬로 알려져 있다. 연산 시간 O(nlog2 n).
퀵 정렬(Quick Sort) 알고리즘
#include
/** 교환 함수 */ void interchange(int &a, int &b) { int temp = a; a = b; b = temp; } void quick_sort(int *ay, int length) { int left, right, key, j; if (length <= 1) return; key = ay[length-1]; // 마지막 값을 키 값으로 설정 for (left = 0, right = length-2;; left++, right–) { /** 키 값 보다 클 때까지 left를 우측으로 이동 */ while (ay[left] < key) left++; /** 키 값 보다 작을 때까지 right를 좌측으로 이동*/ while (ay[right] > key) right–; /** 만일 좌측과 우측이 만난다면 중지*/ if (left >= right) break; interchange(ay[left], ay[right]); // 교환 함수 호출 } interchange(ay[left], ay[length-1]); quick_sort(ay, left); quick_sort(ay+left+1, length-left-1); /** 출력 */ for (j = 0; j < length; j++) printf("%d", ay[j]); printf("\n"); } void main() { int ay[] = {41, 24, 76, 11, 45, 64, 21, 69, 19, 36}; int length; length = sizeof(ay) / 2; quick_sort(ay, length); } 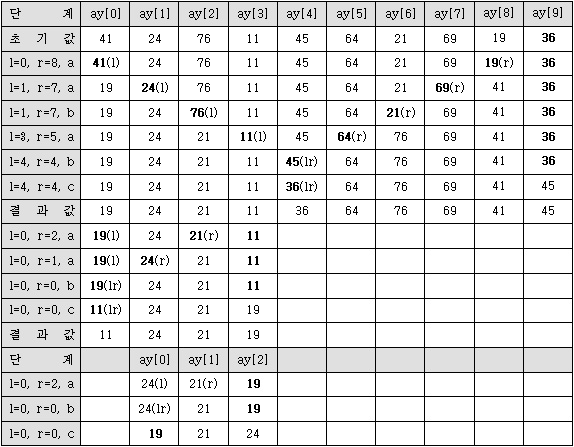
퀵 정렬(Quick Sort) 수행 과정 - 이원 합병 정렬(2-Way Merge Sort): 두 개의 키들을 한 쌍으로 하여 각 쌍에 대하여 순서를 정하고 나서 순서대로 정렬된 각 쌍의 키들을 합병하여 하나의 정렬된 서브 리스트로 만들어 최종적으로 하나의 정렬된 파일이 될 때까지 반복하여 정렬하는 방식. 연산 시간 O(nlog2 n).
- 기수 정렬(Radix Sort): 생략.
- 이진 트리 정렬(Binary Tree Sort): 생략.
- 힙 정렬(Heap Sort): 완전 이진 트리(Binary Tree)인 순서 트리(Ordered Tree) 형태로 데이터를 저장하고 트리 액서스 알고리즘에 의해 부모 노드가 자식 노드 보다 크게 되도록 구성하는데 첫 번째 구성된 형태를 초기 Heap 상태라고 한다. 이 초기 Heap 상태에서 뿌리 노드를 맨 마지막으로 이동시켜 대상 개수를 하나씩 줄여 나가면서 정렬하는 방식. 연산 시간 O(nlog2 n).
② 외부 정렬(External Sort)
- 외부 정렬(External Sort)의 개념
정렬하고자 하는 자료를 보조기억장치에 넣은 후 일부의 자료씩 주기억장치에 옮겨 병합하여 정렬하는 방식으로 자료의 양이 많을 때 사용한다.
- 외부 정렬(External Sort)의 종류
- 합병 정렬(Merge Sort): 입력 파일의 일부를 주기억장치에서 수행하여 적당한 내부 정렬을 수행하는데 이것을 런이라고 한다. 그 후 만들어진 부분을 전체가 합병 형태로 조합해 나간다. 이런 과정은 하나의 런을 얻을 때까지 수행된다.
- 균형 합병 정렬(Balanced Merge Sort): 테이프를 이용하여 합병하는 것으로 n개의 테이프 장치가 주어지면 각 테이프는 똑 같은 크기의 레코드(Record)들이 반반씩 나누어져서 내부 정렬을 통해 처리하는 방법이다.
- 계단식 합병 정렬(Cascade Merge Sort): 균형 합병 방식과 비슷하다. 즉 모든 테이프를 함께 작동하여 초기의 자료 파일을 하나의 테이프를 제외한 나머지 테이프에 분배한 다음 이들의 합병을 반복한다. 작업에서 n개의 테이프 중 1개 테이프라도 합병이 멈추면 작업을 끝내는 방식이다.
- 다상 합병 정렬(Polyphase Merge Sort): 보통 6개 이내의 테이프를 사용하여 분류하는데, 부분 파일을 피보나치 수열에 맞추어 테이프에 분배하여 합병하는 방식이다.
- 오실레이팅 정렬(Oscillation Sort): 테이프를 양쪽 방향으로 읽을 수 있는 성질을 이용한 방식이다.
다. 정렬 방식에 따른 분류
- 비교식 정렬(Comparative Sort): 비교하려고 하는 각 레코드의 키 값들을 한 번에 두 개씩 비교, 교환하여 정렬하는 방법이다. 즉 이 정렬 방식은 1회 1번씩 키를 비교해서 정렬하는 방법으로 크게 두 가지로 나눌 수 있다. 삽입(Insertion), 버블(Bubble), 선택(Selection), 셀(Shell) 정렬 등의 분야와 퀵(Quick), 힙(Heap), 합병(Merge), 이진 트리(Binary Tree) 정렬 등의 분야가 있다. 전자의 경우 알고리즘은 간단하나 연산 시간이 O(n자승)으로 소량의 자료 처리에 좋고, 후자는 알고리즘은 복잡하지만 연산 시간이 O(nlog n)으로 대량의 자료 처리에 적합하다.
- 분산식 정렬(Distributed Sort): 레코드의 키 값을 기준으로 전체 레코드 집합을 다수의 부분 집합으로 분해하는데, 한 부분에 속한 레코드의 키 값은 다른 부분 집합에 속한 레코드의 키 값과 다르게 만든다. 즉 1회 1 digit씩 비교해서 정렬하는 방식으로 기수 정렬(Radix Sort) 등이 여기에 속한다.
- 주소 계산 정렬(Address Calculation Sort): 비교하고자 하는 키 값을 주소(Address)로 변환하여 정렬하는 방식으로 특징은 표(Table)내에 첫 번째 내용을 넣는 속도가 빠르다는 것이다. 표를 채워 감에 따라 새로운 내용을 표에 더하는 시간은 기하 급수적으로 증가한다. 즉 이 방법은 키의 비교에 의해서 정렬하는 것이 아니라 키를 적당한 방법으로 연산을 하여 정렬하는 방식으로 해싱 정렬(Hashing Sort) 등이 있다.
2. 탐색(Search)
가. 탐색(Search)의 정의
기억장소에 기억 중인 특정한 자료를 찾아내는 것을 말한다.
나. 탐색(Search) 장소에 따른 분류
만일 파일이나 테이블이 주기억 장소에 기억되어 있는 것을 찾을 경우는 내부 탐색(Internal Search), 보조기억장치에 있는 것을 찾을 때에는 외부 탐색(External Search)이라고 한다.
- 내부 탐색(Internal Search)의 종류
- 순차 탐색(Sequential Search): 대상 자료를 순서대로 하나씩 비교해서 원하는 자료를 찾는 검색 방식으로 자료가 정렬되어 있지 않고 대상 범위를 알 수 없을 때 사용.
순차 탐색(Sequential Search) 알고리즘
#include
int seq_srch(int *ay, int length, int key) { int i; for (i=0; i < length; i++) { if (ay[i] == key) return(i); } return(-1); } void main(void) { int ay[] = {77, 33, 44, 11, 88, 22, 66, 55}; int length, key, res; length = sizeof(ay) / 2; key = 11; res = seq_srch(ay, length, key); if (res == -1) { puts("검색 결과가 없습니다."); } else { printf("찾으시는 값은 %d 번째 있습니다.\n", res); } } - 제어 탐색(Controlled Search): 대상 자료가 정렬되어 있고 대상 자료에 대한 범위를 알고 있을 때 적용할 수 있다.
- 이진 탐색(Binary Search): 대상 범위를 절반씩 축소시키면서 찾고자 하는 값을 대상 자료의 중간 값과 비교하여 작은 부분을 버리는 식으로 원하는 데이터를 찾는 방식이다.- 피보나치 탐색(Fibonacci Search): 피보나치 수열을 이용하여 탐색하는 방식으로 앞에 있는 자료일수록 오버 헤드가 심하고 더하기 빼기만 가지고도 탐색 가능한 방식이다. 이진 탐색(Binary Search) 보다 평균 효율이 좋다.
- 보간 탐색(Interpolation Search): 데이터가 있음직한 부분을 보간해서 탐색하는 방식으로 사전식 탐색이라고도 한다.
- 블록 탐색(Block Search): 데이터를 블록을 묶어 구성하고 블록을 결정할 때는 인덱스(Index)를 사용하고 해당 블록 내부에서는 순차 탐색(Sequential Search)을 사용하여 탐색하는 방식이다.
- 이진 탐색 트리(Binary Search Tree): 데이터를 입력되는 순서에 따라 첫 번째 데이터는 뿌리 노드(Root Node), 다음 데이터부터는 뿌리 노드(Root Node)와 비교하여 뿌리 노드(Root Node) 보다 작으면 좌측에 연결하고 크면 우측에 연결하여 이진 트리로 구성한 다음 같은 방식으로 탐색하는 방식이다.
- 외부 탐색(External Search)의 종류
생략.
3. 해싱(Hashing)
가. 해싱(Hashing)의 정의
각 레코드들의 키의 계수적(計数的)인 성질을 이용하여, 계산에 의해서 키에서 주소로 직접 변환하는 방식으로 주소를 기억 공간에 보관하거나 탐색하는 것을 말한다.
나. 해싱(Hashing)의 용어
- 해싱 함수(Hashing Function): 키 값을 변환하여 레코드(Record)를 저장할 주소를 산출하는 명령을 하나의 수식으로 표현하는 방법.
- 버킷(Bucket): 하나의 주소를 가지면서 한 개 이상의 레코드(Record)를 저장할 수 있는 공간.
- 슬롯(Slot): 한 개의 레코드(Record)를 저장할 수 있는 공간으로 N개의 슬롯(Slot)이 모여 버킷(Bucket)을 형성.
- 충돌(Collision): 해싱 함수(Hashing Function)에 의해서 계산된 홈 주소가 같은 경우에 벌어지는 충돌 현상.
- 시노님(Synonym): 같은 홈 주소를 갖는 레코드(Record)의 집합.
- 오버플로우(Overflow): 해당 버킷(Bucket)에 더 이상의 레코드(Record) 키 값을 기억시킬 수 없어서 넘쳐 나는 현상.
다. 해싱 함수(Hashing Function)의 종류
- 제산법(Division method): 키 값을 특정한 소수로 나누어서 나머지 값을 주소로 이용하는 방법.
- 제곱법(Mid-square method): 키 값을 제곱하고 이 값의 중간에서 적당한 몇 개의 비트를 주소로 채택하는 방법.
- 폴딩법(Folding method): 키를 여러 부분으로 나누는데 대략 2개나 3개로 나누어 각 부분을 더하거나 일정 구간을 접고(folding) 더해서 주소를 얻는 방법으로 이동 폴딩(Shift folding)과 경계 폴딩(Boundary folding)이 있다.
예로 12320324111220는 키를 3개씩 5부분, 즉 P1=123, P2=203, P3=241, P4=112, P5=20으로 나눈다. 이것을 이동 폴링(Shift folding)로 처리하면 P1+P2+P3+P4+P5=699의 값을 해싱 번지로 얻을 수 있다. 또 경계 폴링(Boundary folding)로 처리하면 P1+P2*+P3+P4*+P5=897의 값을 얻을 수 있다. 단, *은 각 값의 접지(摺紙, folding)로 P2는 302, P4는 211가 된다.
- 기수 변환법(Radix conversion method): 진법으로 표현된 주어진 키를 다른 진법으로 가정하고, 키를 변환하여 주소를 얻는 방법.
- 무작위법(Random method): 키의 주소를 무작위(Random)로 산출하는 방법. 만약 충돌이(Collision)이 발생한다면 다음 무작위 수(Random number)를 이용한다.
- 계수 분석법(Digit analysis method): 구성하는 모든 키들을 파악해서 분포가 비교적 고른 자리를 필요한 만큼 택하여 키의 주소로 삼는 방법. 이 방식은 매우 간단하나 번번히 충돌이 발생할 수 있으므로 오버플로우(Overflow)를 야기할 수 있다.
라. 해싱(Hashing)의 충돌(Collision) 및 오버플로우(Overflow) 처리
해싱(Hashing)의 단점은 다른 키를 사용하여 해시 함수를 구성하였더라도 같은 번지로 연결되는 충돌(Collision)이 발생되는 경우가 존재한다는 것이다. 이처럼 해싱 함수(Hashing function)에 의해서 더 이상 레코드(Record)를 보관할 수 없는 것을 오버플로우(Overflow)라고 한다.
- 선형 방법(Linear method): 충돌(Collision)과 오버플로우(Overflow)가 발생 되었을 때, 그 다음 빈 버킷(Bucket)에 레코드(record)를 저장하는 방법.
- 무작위 방법(Random method): 무작위 수(random number)를 통해서 충돌(Collision)을 해결하는 방법.
- 이차 방법(Quadratic quotient method): 충돌(Collision) 발생시 이차 함수의 증가치를 더한 후 해싱 테이블(Hashing table)의 크기로 나누어 처리하는 방식.
- 체인 방법(Chaining method): 충돌(Collision)이 발생시 빈 버킷(Bucket)에 레코드(Record)를 저장하고 연결 리스트(Linked List)로 연결시켜 보관하는 방식.
Ⅴ. 파일조작기법
1. 파일(File)의 정의
어떤 프로그램에 의하여 사용되는 데이터의 집합 또는 사용자에 의하여 작성된 문서 등, 일정한 규칙에 의해 기록된 관련 있는 정보의 완전한 집합체로서 고유의 이름이 할당되어 있으며 하드 디스크(Hard Disk) 등의 보조기억장치에 저장되어 있는 것을 말한다.
2. 파일(File)의 기록 매체
가. 보조기억장치
① 자기 테이프(Magnetic Tape)
얇고 좁은 플라스틱 테이프 표면에 자성체를 발라 정보를 저장할 수 있게 한 매체. 동그란 릴에 감겨 있으며 테이프 드라이브에 걸어서 사용한다. 기억 용량이 크고 값이 싸며, 속도도 빠르다. 그러나 순차 접근(Sequential access)밖에 할 수 없기 때문에 디스크와 같은 직접 접근 기억 장치(Direct access storage device)보다는 느리고, 사용하기도 불편하므로 근래에는 주로 대용량의 정보를 오랫동안 저장하는 데 사용된다.
② 자기 디스크(Magnetic Disk)
보통 레코드 판과 같은 원판을 여러 장 동일 축에 고정시키고 그 판의 양면에 정보를 기록하는 디스크. 정보의 기록과 읽기는 각 면에 1개의 자기 헤드(Magnetic Head)가 있어 회전하는 면 위로 이동하면서 한다. 자기 디스크(Magnetic Disk)는 안정된 고밀도 기록을 할 수 있고 기록 직후 재생이 가능하다. 또 정보의 업데이트나 제거가 가능하고 전원이 끊겨도 정보가 보전되는 비휘발성 매체이며, 가격에 비해 성능이 비교적 양호한 편이다.
3. 파일(File)의 편성 방법
가. 순차 파일(Sequential File)
- 순차 파일(Sequential File)의 개념
모든 컴퓨터에 쉽게 적용할 수 있는 가장 대중적인 방법으로, 레코드(Record)들이 하나 또는 그 이상의 키 필드 값에 따라 차례로 연속되게 저장하는 방법. 대량의 정보를 가진 파일을 쉽게 만들기 위해 사용하며, 테이프를 많이 사용하지만 디스크나 드럼도 가능하다.
- 순차 파일(Sequential File)의 장점
- 레코드(Record)가 키 순으로 배열해 있기 때문에 액세스 순서를 순차적으로 한다면 액세스 시간이 상당히 빠르다.
- 일괄 처리(Batch Processing)에 적합하다.
- 순차 파일(Sequential File)의 단점
- 임의 접근(Random access)할 경우 효율이 떨어진다.
- 레코드(Record) 삽입 시 파일 전체의 복사가 필요하다.
나. 색인 순차 접근 방식(ISAM, Indexed sequential access method)
- 색인 순차 접근 방식(ISAM)의 개념
이는 레코드(Record)들을 블록 단위로 나누어 한 블록 안에서는 순차적으로 수록하고, 블록 별로 시작 레코드의 위치를 기록한 인덱스 파일(Indexed File)을 구성하여 키 값이 주어지면 이 인덱스(Index)를 기준으로 그 레코드를 빨리 찾아낼 수 있도록 한다. 즉 순차 파일(Sequential File)과 직접 편성 파일(Direct File)을 혼합한 방식이다. 만일 한 블록 내에 레코드들이 다 차면 오버플로우 영역(Overflow area)에서 블록을 할당 받아 연결시킨다. 이는 레코드의 검색 속도가 매우 빠르고, 삽입이나 삭제도 쉬워 대용량의 데이터베이스에 필수적인 기술이다. 색인을 구성하는 방법에는 주로 B 트리(B Tree)가 많이 사용된다.
- 색인 순차 접근 방식(ISAM)의 장점
- 순차 접근(Sequential access)과 직접 접근이 가능.
- 레코드(Record)의 추가 삽입시 파일 전체의 복사가 필요 없다.
- 색인 순차 접근 방식(ISAM)의 단점
- 색인(Index)이나 오버플로우(Overflow)의 공간이 요구된다.
- 오버플로우(Overflow) 레코드(Record)가 많은 경우 그 부분을 위한 접근 시간이 필요하다.
- 추가 삭제의 횟수가 많아질 경우 효율이 떨어진다.
- 색인 순차 접근 방식(ISAM)의 구성
- 기본 자료 영역(Prime data area): 실제 데이터가 기록되는 부분.
- 인덱스 영역(Index area): 기본 자료 영역(Prime data area)에 대한 색인(Index)을 구성하는 부분.
- 트랙 색인(Track Index): 가장 작은 단위의 색인.
- 실린더 색인(Cylinder Index): 트랙 색인(Track Index)에 대한 색인.
- 마스터 색인(Master Index): 실린더 색인(Cylinder Index)에 대한 색인.
- 오버플로우 영역(Overflow area): 기본 자료 영역(Prime data area)에 기록되지 못하고 넘친 데이터를 기록하는 부분.
- 실린더 오버플로우 영역(Cylinder Overflow area): 하나의 실린더 색인(Cylinder Index) 범위마다 두는 오버플로우 구역.
- 독립 오버플로우 영역(Independent Overflow): 실린더 오버플로우 영역(Cylinder Overflow area)에 다시 오버플로우(Overflow)가 발생한 경우에 기록하는 부분.
다. 가상 기억 접근 방식(VSAM, Virtual Storage Access Method)
색인 순차 접근 방식(ISAM)에서 오버플로우 영역(Overflow area)을 제외한 방식. 즉 색인 순차 접근 방식(ISAM) 은 정적 인덱스 편성을 하는데 반해 가상 기억 접근 방식(VSAM)은 동적 인덱스 편성을 하여 오버플로우 영역(Overflow area)을 두지 않고 미리 예비 구역(Virtual Storage)을 두어 삽입이 일어나게 되면 예비 구역(Virtual Storage)을 사용하는 방식이다.
라. 직접 편성 파일(Direct File)
- 직접 편성 파일(Direct File)의 개념
레코드(Record)가 가지고 있는 키를 사용해서 접속할 수 있는 파일 형식. 데이터를 파일(File)에 넣을 때나 파일(File)에 접속 할 때는 먼저 레코드(Record)의 키를 해싱 함수(Hashing Function)를 이용해 주소로 변환한 후에, 변환된 주소를 사용해서 레코드(Record)를 넣거나 레코드(Record)에 접속한다.
- 직접 편성 파일(Direct File)의 장점
- 대화식 처리에 이용할 수 있다.
- 레코드(Record)를 순차 파일(Sequential File)에서처럼 복사할 필요 없이 바로 갱신 가능하며, 레코드의 검색, 삭제, 수정 등이 가능하다.
- 직접 편성 파일(Direct File)의 단점
- 순차적인 검색이 불가능하다.
마. 역파일(Inverted File)
- 역 파일(Inverted File)의 개념
파일(File)이나 데이터베이스(Database)에서 레코드(Record)를 빨리 검색하기 위해 별도의 색인 파일(Indexed File)을 만드는 것. 이때 색인 파일에는 검색의 기준이 되는 키 필드의 값과 그 키 값을 가지는 레코드에 대한 지시자(Pointer)들이 저장되며, 원래 파일에서는 그 키 값이 빠진다.
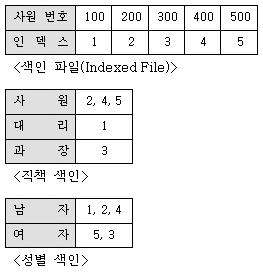
- 역 파일(Inverted File)의 장점
- 레코드(Record)를 찾는 질의(Query) 에 만족하는 레코드(Record)를 탐색할 경우, 한 번씩만 접근하면 된다.
- 레코드(Record)의 삽입과 삭제가 비교적 쉽다.
- 자료 파일에 접근하지 않고도 질의(Query)에 응답할 수 있다.
- 탐색 속도가 빠르다.
- 역 파일(Inverted File)의 단점
- 색인(Index)의 각 항의 길이가 가변적이다.
- 색인(Index)을 다루기가 어려워진다.
바. 다중 리스트 파일(Multi-List File)
- 다중 리스트 파일(Multi-List File)의 개념
각 키에 대해서 인덱스(Index)를 만든 다음 각 레코드를 여러 개의 리스트에 속하도록 만든 파일 시스템이다.
- 다중 리스트 파일(Multi-List File)의 장점
- 색인(Index)의 각 항의 길이가 고정적이다.
- 연속적이고 전체적인 탐색에 효율이 좋다.
- 다중 리스트 파일(Multi-List File)의 단점
- 역 파일(Inverted File)은 색인(Index)으로만 응답할 수 있으나, 다중 리스트는 자료 레코드에 직접 접근해야 한다.
끝
참고 자료
正益社 – 전산학 개론
한올출판사 – C언어로 구성한 자료구조
가메출판사 – 정보처리기사 필기 7년간 기출문제 총정리
정보통신용어사전